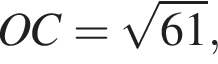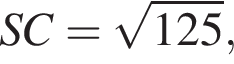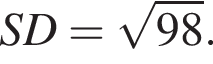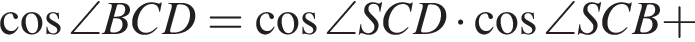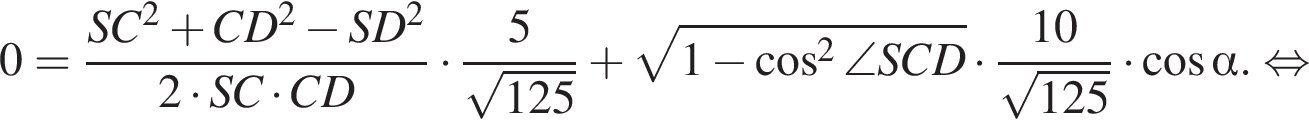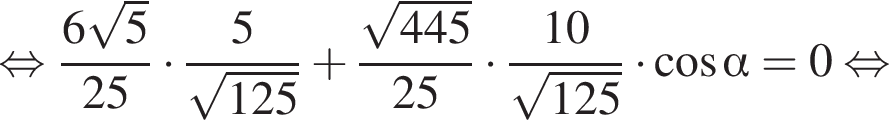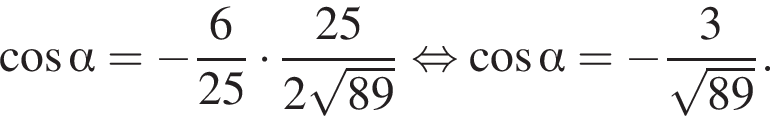Среди точек 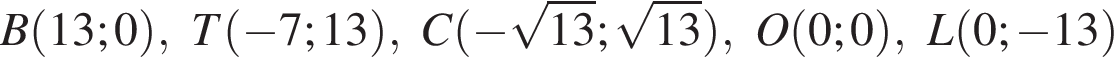 выберите ту, которая принадлежит графику функции, изображённому на рисунке:
выберите ту, которая принадлежит графику функции, изображённому на рисунке:
Одно число меньше другого на 64, что составляет 16% большего числа. Найдите меньшее число.
Образующая конуса равна 26 и наклонена к плоскости основания под углом 60°. Найдите площадь боковой поверхности конуса.
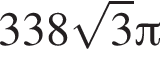

Значение выражения 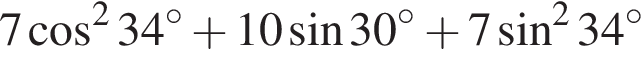 равно:
равно:
Две окружности с центрами A и B касаются в точке M. Найдите длину отрезка CN, если
 и диаметр большей окружности на 25 больше радиуса меньшей окружности.
и диаметр большей окружности на 25 больше радиуса меньшей окружности.
Через вершину A прямоугольного треугольника ABC (∠C = 90°) проведен перпендикуляр AK к его плоскости. Найдите расстояние от точки K до прямой BC, если AK = 2, AB = 4, BC = ![]()
Сократите дробь 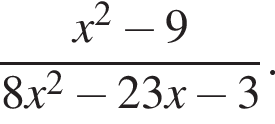
Сумма всех натуральных решений неравенства 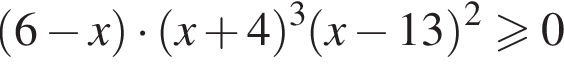 равна:
равна:
Найдите значение выражения 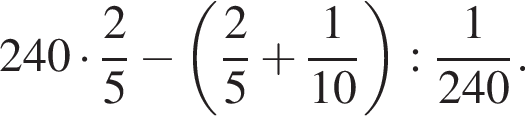
Укажите номер квадратного уравнения, корнями которого являются числа x1 − 1, x2 − 1, где x1, x2 — корни квадратного уравнения 3x2 − 5x − 6 = 0.
1) x2 + x − 6 = 0;
2) 3x2 − 11x + 8 = 0;
3) 3x2 − x − 8 = 0;
4) 3x2 + 11x + 8 = 0;
5) 3x2 + x − 8 = 0.
Найдите количество всех целых решений неравенства 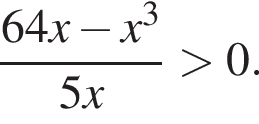
Найдите произведение большего корня на количество корней уравнения 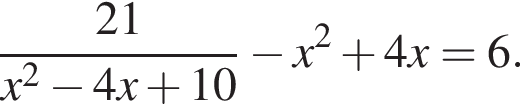
Выберите все верные утверждения, являющиеся свойствами нечетной функции ![]() определённой на
определённой на  и заданной формулой
и заданной формулой 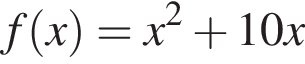 при
при ![]()
1. Функция имеет три нуля.
2. Функция убывает на промежутке [6; 9].
3. Максимум функции равен 25.
4. Минимальное значение функции равно -25.
5. 
6. Функция принимает отрицательные значения при 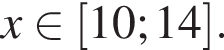
7. График функции симметричен относительно оси абсцисс.
Ответ запишите в виде последовательности цифр в порядке возрастания. Например: 123.
Выберите три верных утверждения:
1) если 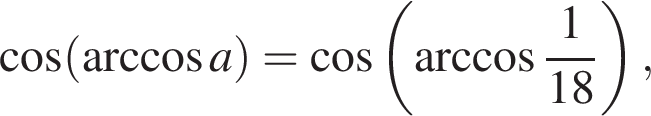 то
то 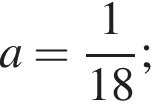
2) если 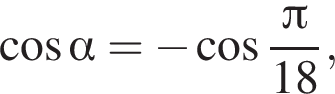 то
то 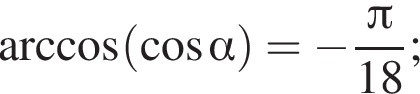
3) если 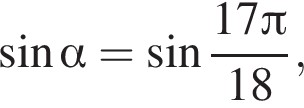 то
то 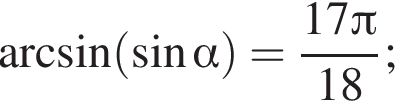
4) если 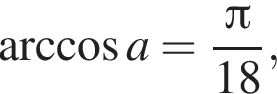 то
то 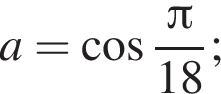
5) если 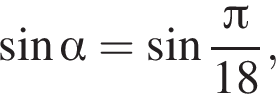 то
то 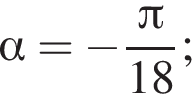
6) если 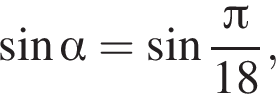 то
то 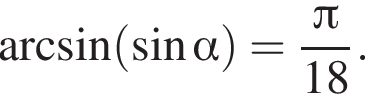
Ответ запишите цифрами (порядок записи цифр не имеет значения). Например: 123.
Градусная мера угла ABC равна 126°. Внутри угла ABC проведен луч BD, который делит данный угол в отношении 1 : 6 (см. рис.). Найдите градусную меру угла 1, если BO — биссектриса угла DBC.
Выберите верные утверждения:
1) число 599 кратно числу 3;
2) число 387 кратно числу 9;
3) число 655 кратно числу 10;
4) число 456 кратно числу 4;
5) число 242 кратно числу 6;
6) число 890 кратно числу 5.
Ответ запишите цифрами (порядок записи цифр не имеет значения). Например: 123.
Дана арифметическая прогрессия −48; −40; −32; ... . Для начала каждого из предложений А−В подберите его окончание 1−6 так, чтобы получилось верное утверждение.
A) Разность этой прогрессии равна ...
Б) Четвертый член этой прогрессии равен ...
В) Сумма шести первых членов этой прогрессии равна ...
1) −24
2) 0
3) 8
4) −160
5) −8
6) −168
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например, А1Б1В4.
Найдите периметр правильного шестиугольника, меньшая диагональ которого равна ![]()
Найдите произведение наибольшего целого отрицательного и наибольшего целого положительного решений неравенства
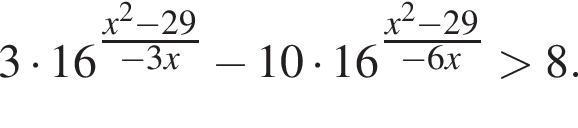
Найдите сумму всех целых решений неравенства 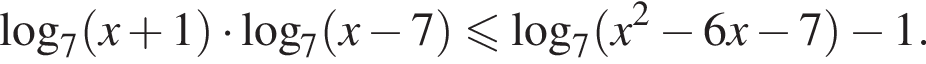
Пусть 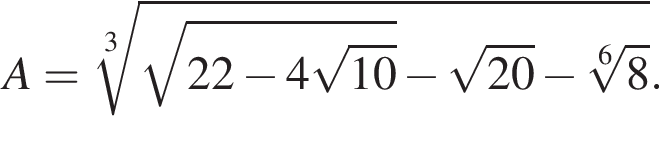 Найдите значение выражения A12.
Найдите значение выражения A12.
Биссектриса угла А параллелограмма ABCD пересекает сторону ВС в точке К так, что ВК = 2, СК = 3. Найдите значение выражения S2, где S — площадь параллелограмма ABCD, если величина угла А равна 60°.
Пусть (x1; y1), (x2; y2) — решения системы уравнений 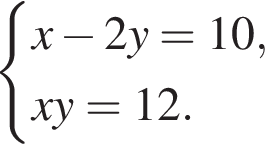 Найдите значение выражения
Найдите значение выражения 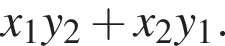
В равнобедренной трапеции диагональ перпендикулярна боковой стороне. Найдите значение выражения ![]() где S — площадь трапеции, если большее основание трапеции равно
где S — площадь трапеции, если большее основание трапеции равно ![]() а один из углов трапеции равен 60°.
а один из углов трапеции равен 60°.
Найдите сумму целых значений x, принадлежащих области определения функции
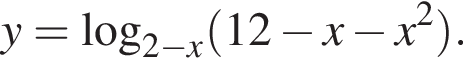
Куб вписан в правильную четырехугольную пирамиду так, что четыре его вершины находятся на боковых ребрах пирамиды, а четыре другие вершины — на ее основании. Длина стороны основания пирамиды равна 1, высота пирамиды — 3. Найдите площадь S поверхности куба. В ответ запишите значение выражения 8S.
Найдите все пары (m, n) целых чисел, которые связаны соотношением m2 + 2m = n2 + 6n + 13. Пусть k — количество таких пар, m0 — наименьшее из значений m, тогда значение выражения k · m0 равно ... .
Найдите (в градусах) наибольший корень уравнения
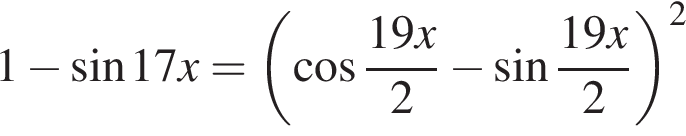
Найдите произведение корней уравнения 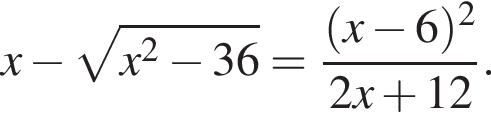
На стороне AB параллелограмма ABCD отмечена точка O так, что 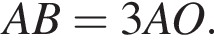 К плоскости ABCD из точки O восстановлен перпендикуляр SO длиной 8. Найдите значение выражения
К плоскости ABCD из точки O восстановлен перпендикуляр SO длиной 8. Найдите значение выражения 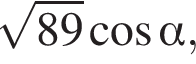 где
где ![]() — линейный угол двугранного угла BSCD, если
— линейный угол двугранного угла BSCD, если 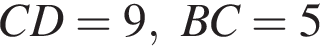 и известно, что площадь ABCD равна 45.
и известно, что площадь ABCD равна 45.

 представляет собой прямую, проходящую через точки вида
представляет собой прямую, проходящую через точки вида 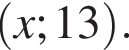 Таким образом, единственное подходящее решение — точка T.
Таким образом, единственное подходящее решение — точка T.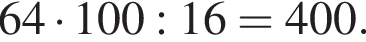 Таким образом, меньшее число
Таким образом, меньшее число 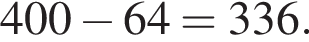
 где r — радиус основания, l — образующая. Найдем радиус:
где r — радиус основания, l — образующая. Найдем радиус:  Таким образом, площадь боковой поверхности равна:
Таким образом, площадь боковой поверхности равна: 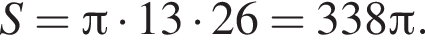

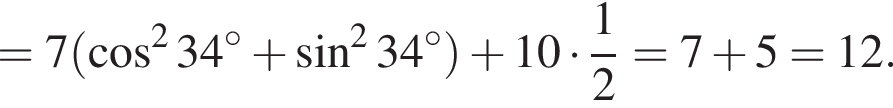
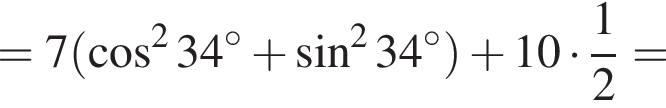
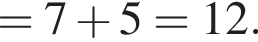
 Значит, длина отрезка
Значит, длина отрезка 
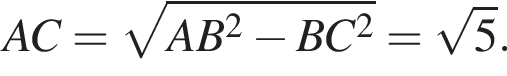 Заметим, что AC является проекцией наклонной KC на плоскость ABC и AC
Заметим, что AC является проекцией наклонной KC на плоскость ABC и AC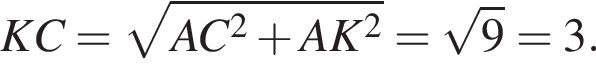
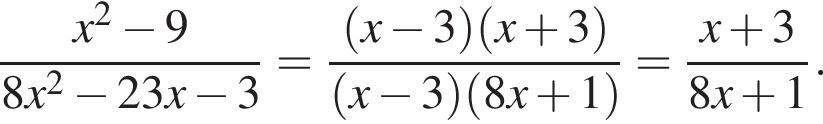
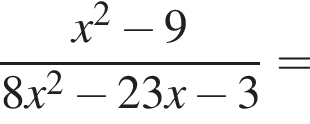
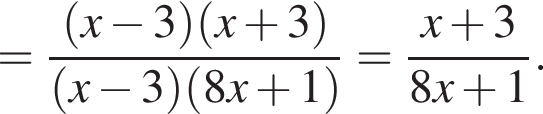
 и при
и при 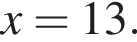 Натуральными решениями являются числа 1, 2, 3, 4, 5, 6, 13. Их сумма равна 34.
Натуральными решениями являются числа 1, 2, 3, 4, 5, 6, 13. Их сумма равна 34.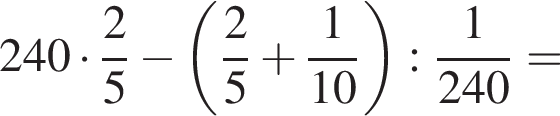
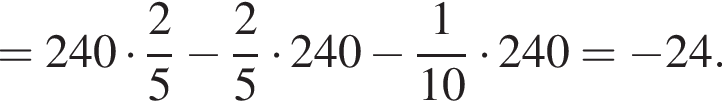
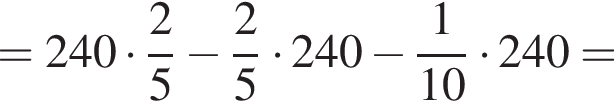
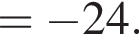
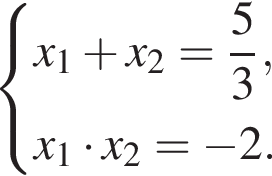
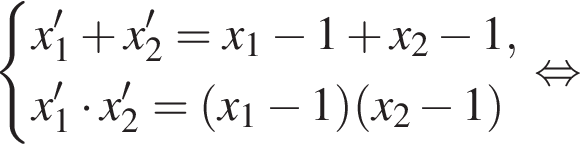
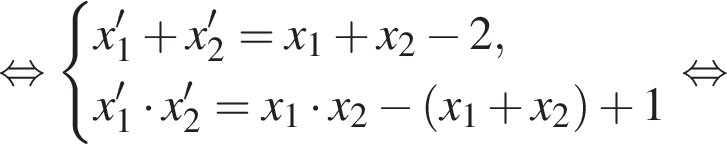
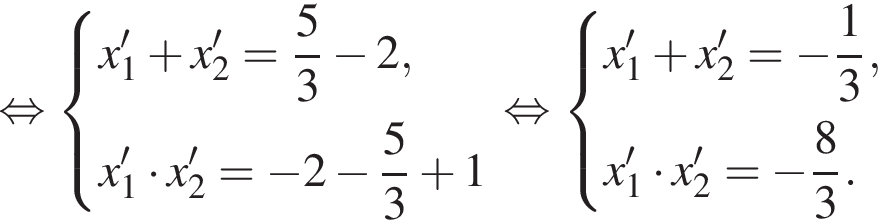
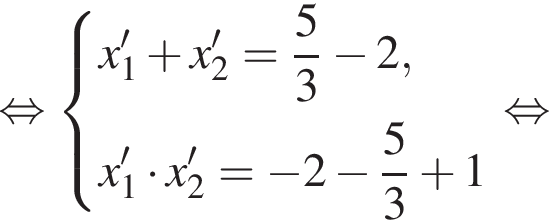
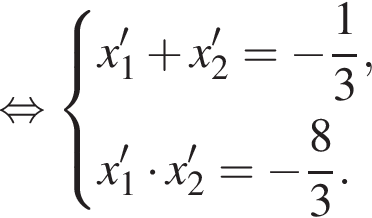
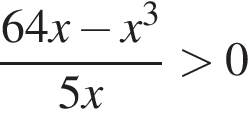
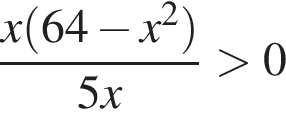
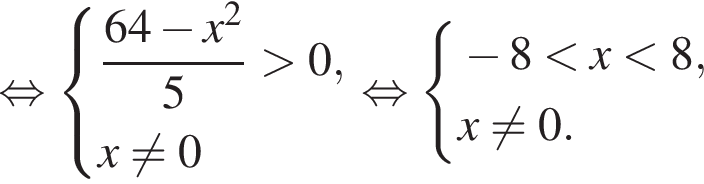
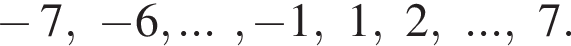
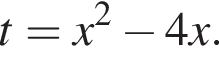 Тогда:
Тогда: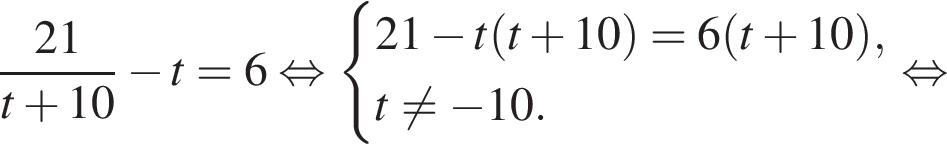
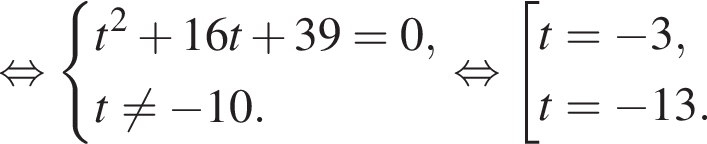
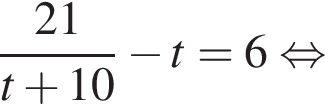
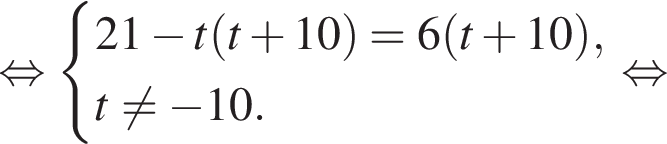
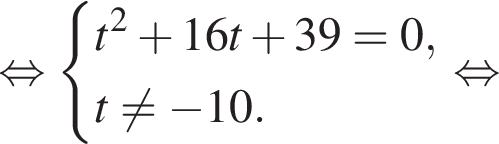
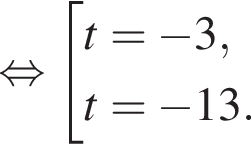
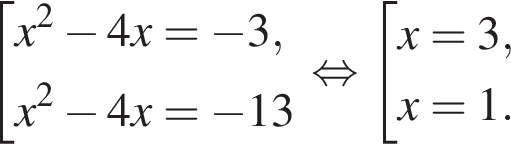
 при
при 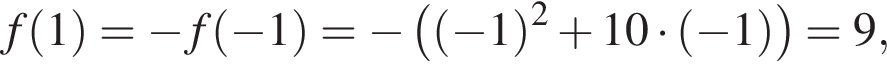
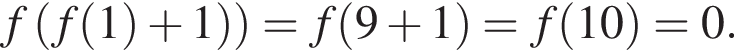 Утверждение 5 верно.
Утверждение 5 верно.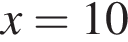 функция равна нулю, а значит, принимает отрицательные значения не во всех точках отрезка
функция равна нулю, а значит, принимает отрицательные значения не во всех точках отрезка 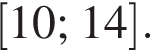 Утверждение 6 неверно.
Утверждение 6 неверно.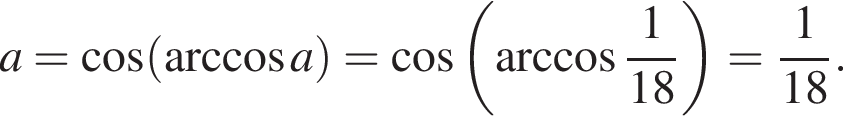

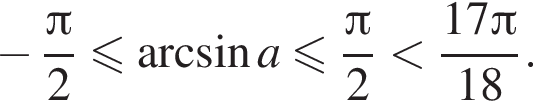
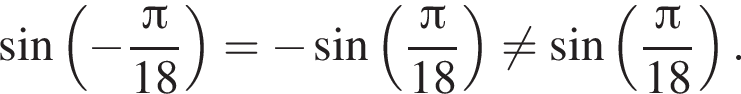
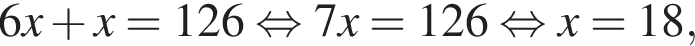
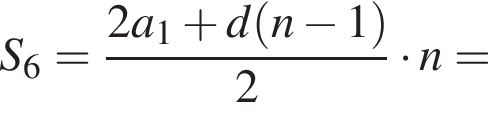
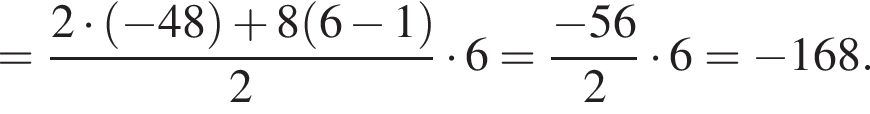
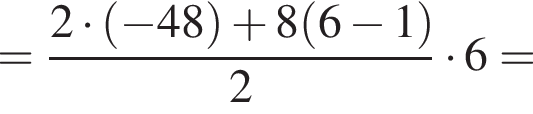
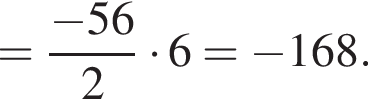
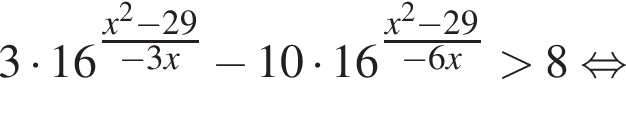
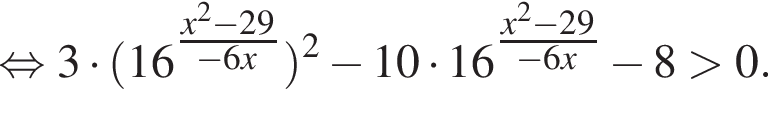
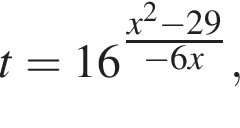 тогда имеем:
тогда имеем: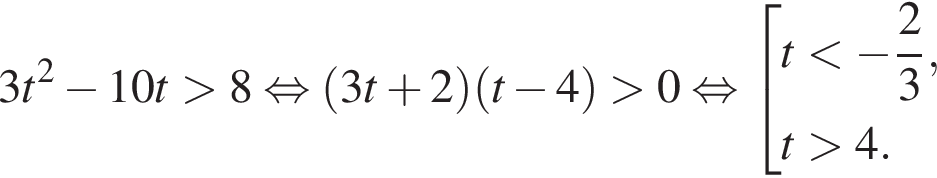
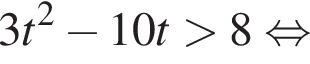
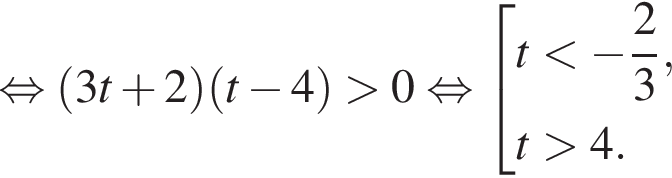
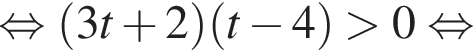
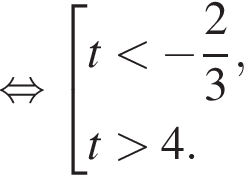
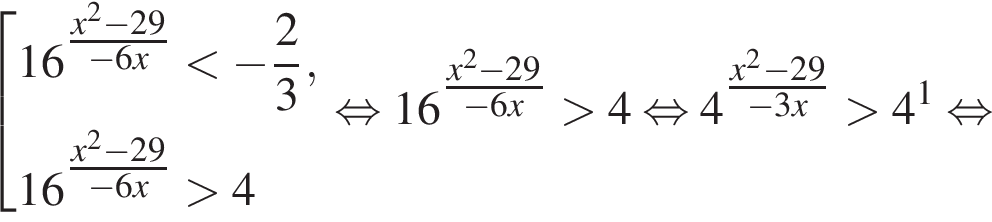
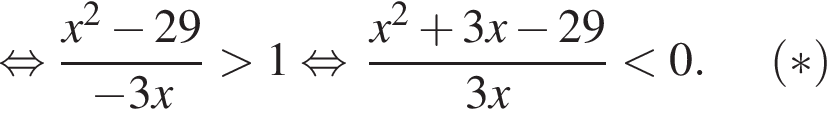
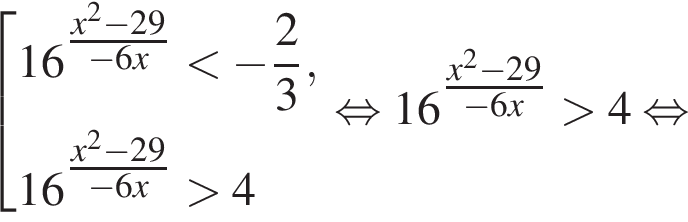
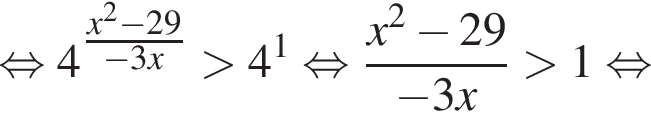
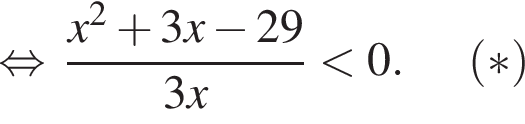
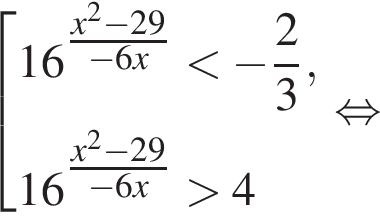
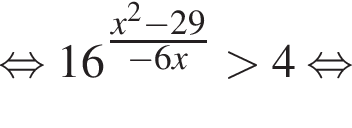
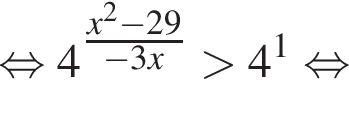
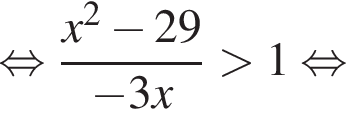
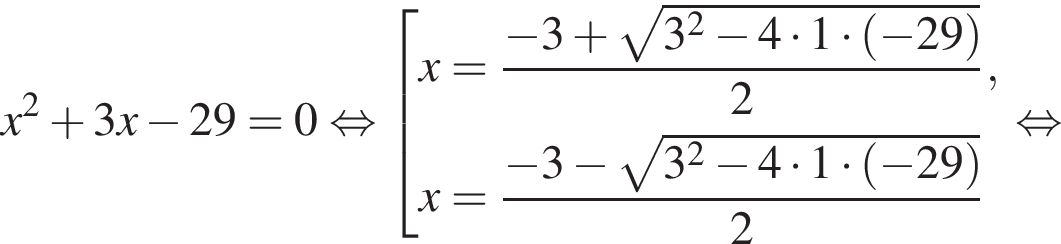
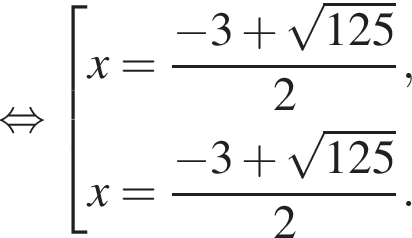
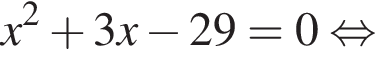
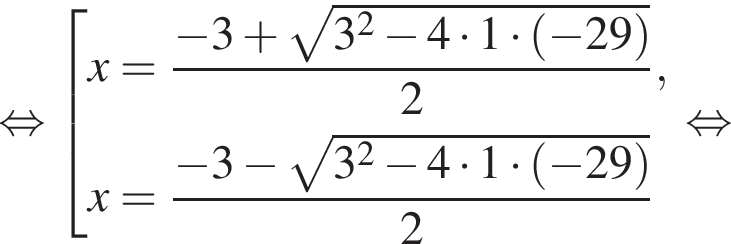
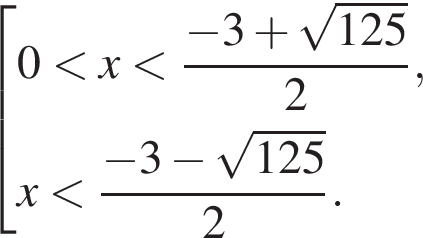
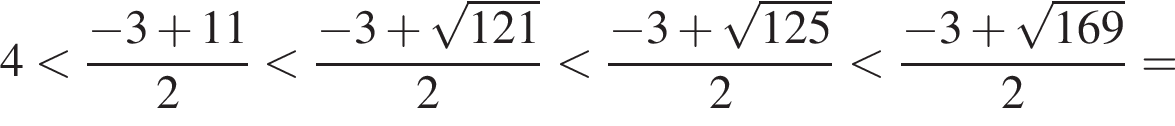
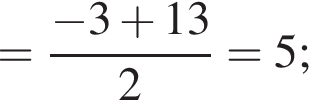
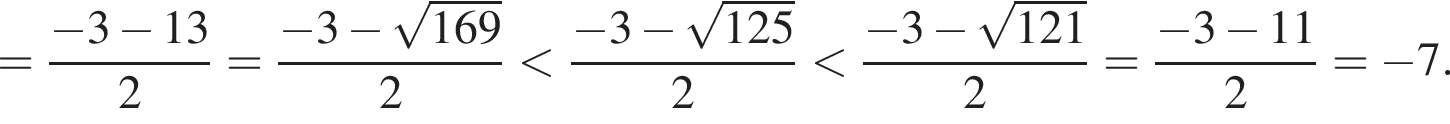
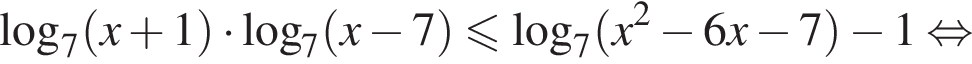
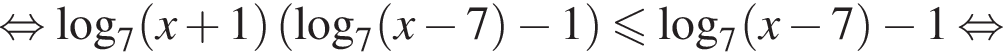
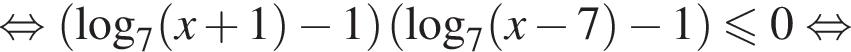
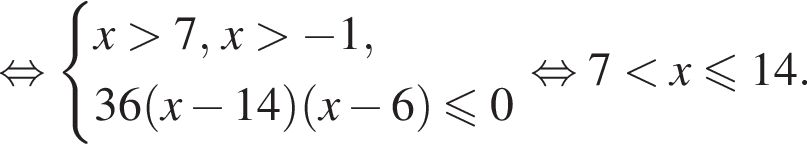

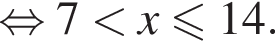
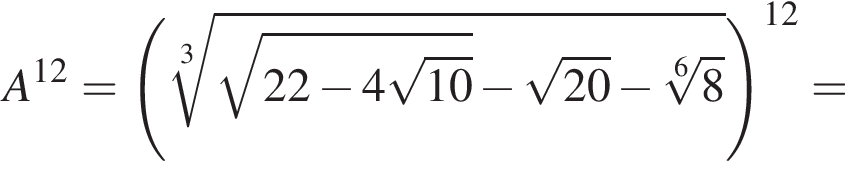
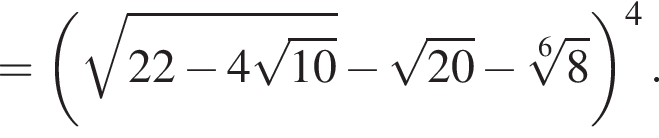
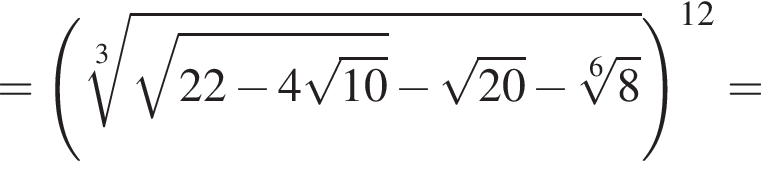
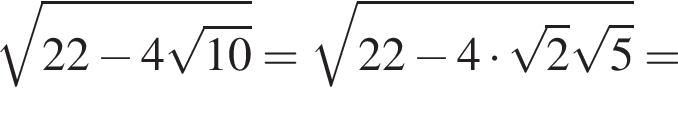
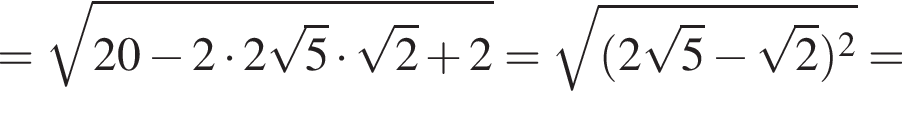
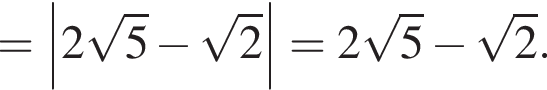
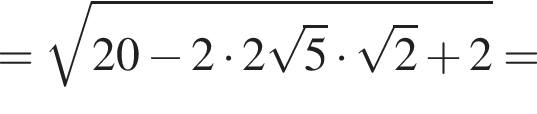
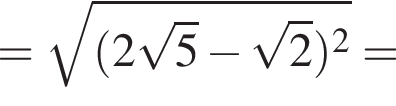
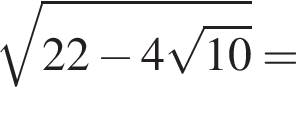
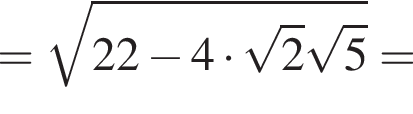
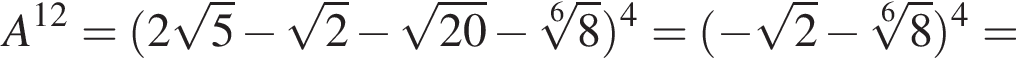
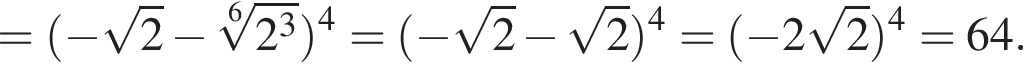
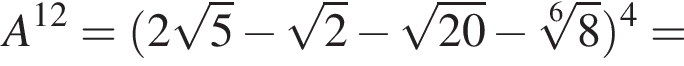
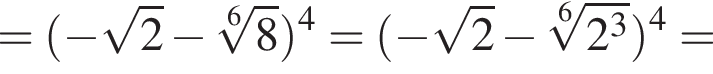
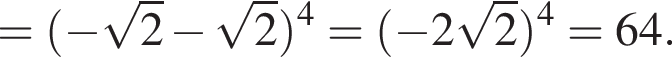
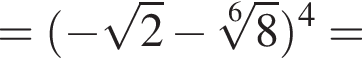
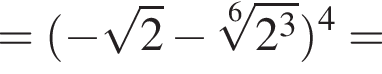
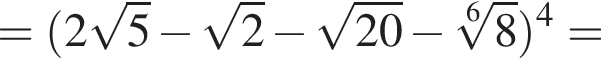
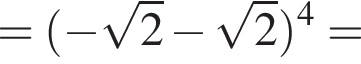
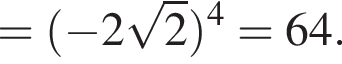
 где первое равенство равно из-за биссектрисы, второе — накрест лежащие углы. Значит, треугольник ABK равнобедренный и потому AB = 2. Далее,
где первое равенство равно из-за биссектрисы, второе — накрест лежащие углы. Значит, треугольник ABK равнобедренный и потому AB = 2. Далее, 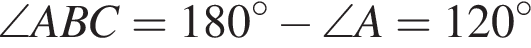 и потому площадь параллелограмма равна
и потому площадь параллелограмма равна 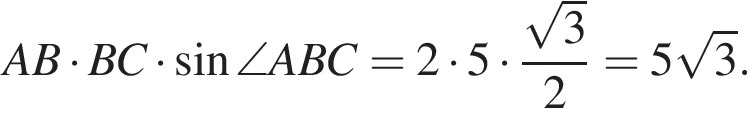
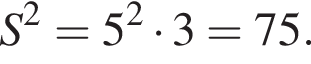
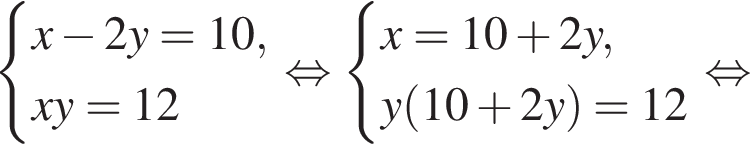
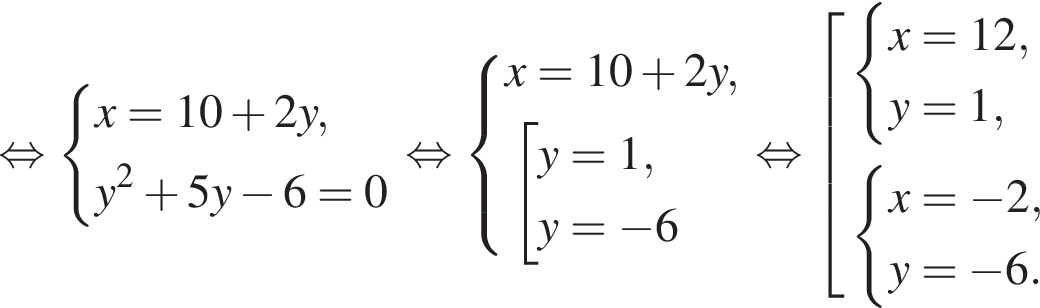
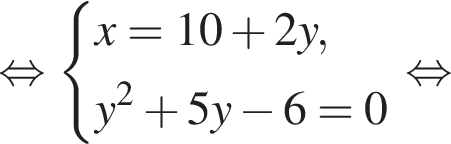
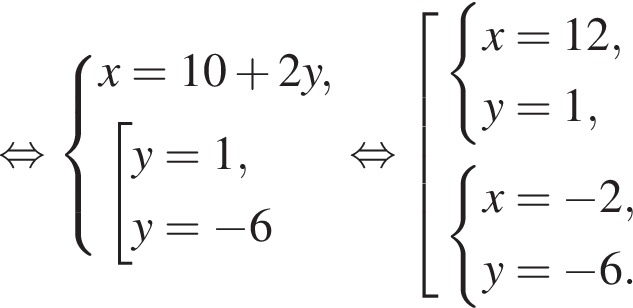
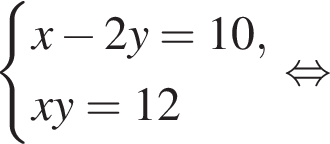
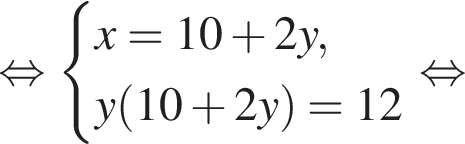
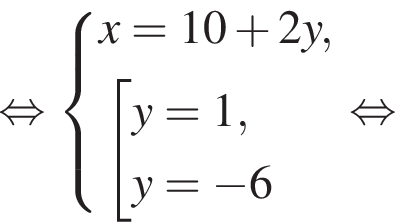
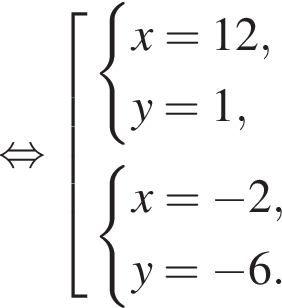
 равно
равно 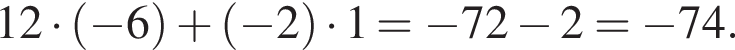
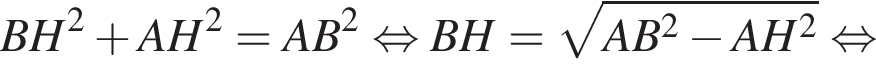
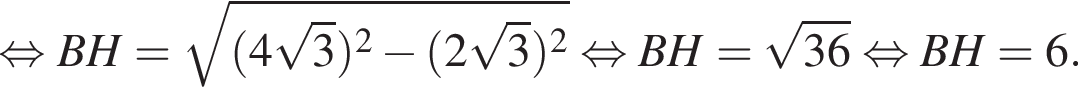
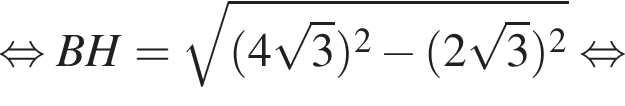
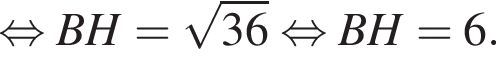
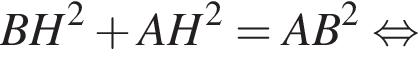

 тогда
тогда 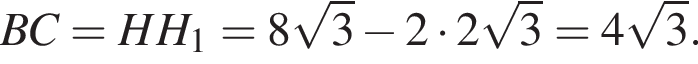
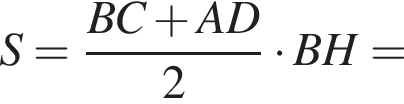
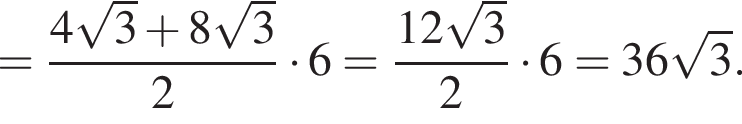
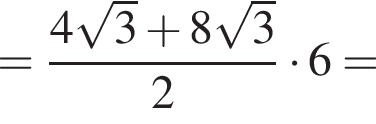
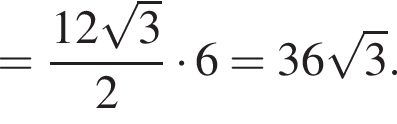
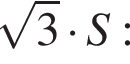

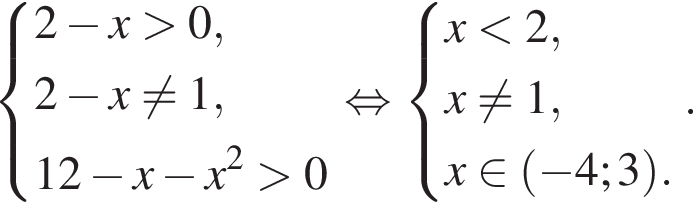
 Их сумма:
Их сумма: 
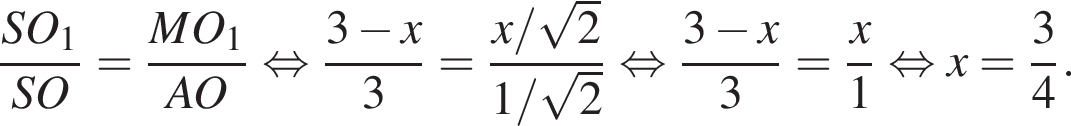
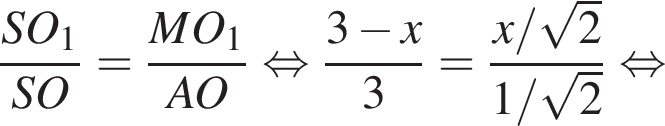
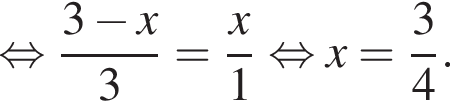
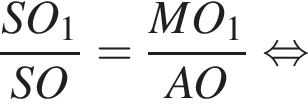
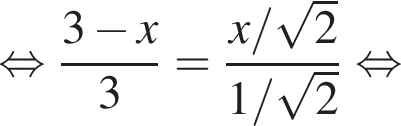
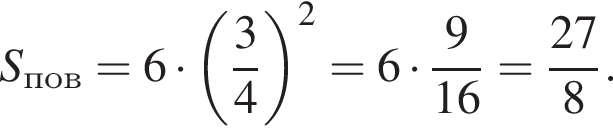
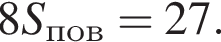
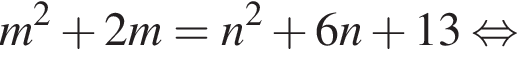
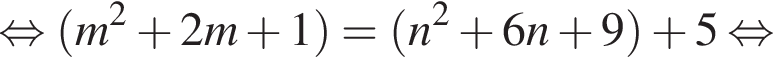
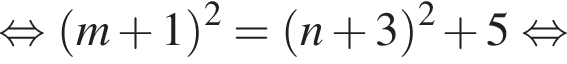

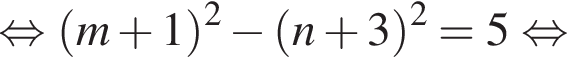

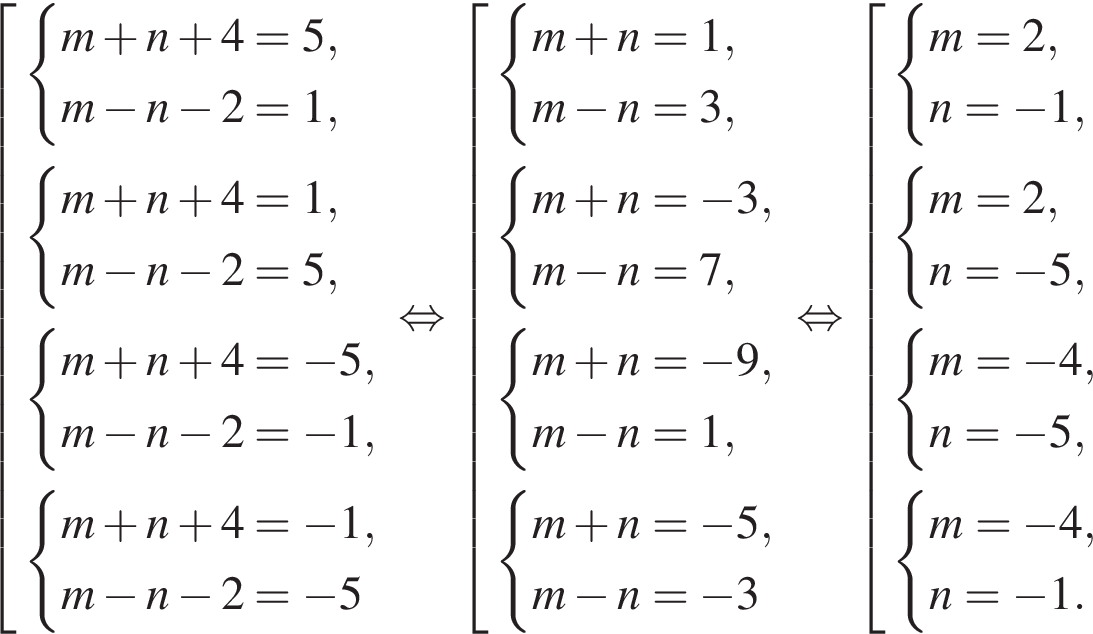
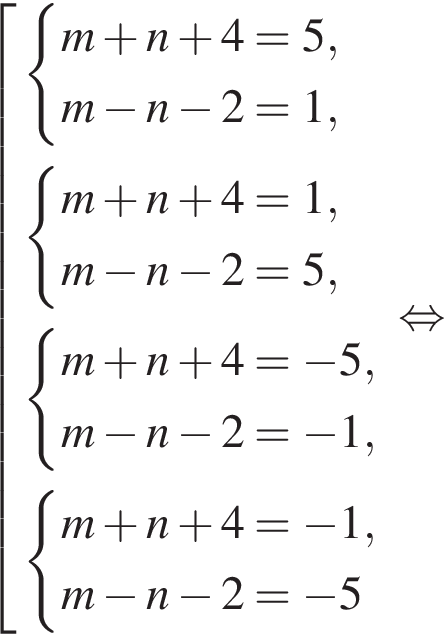
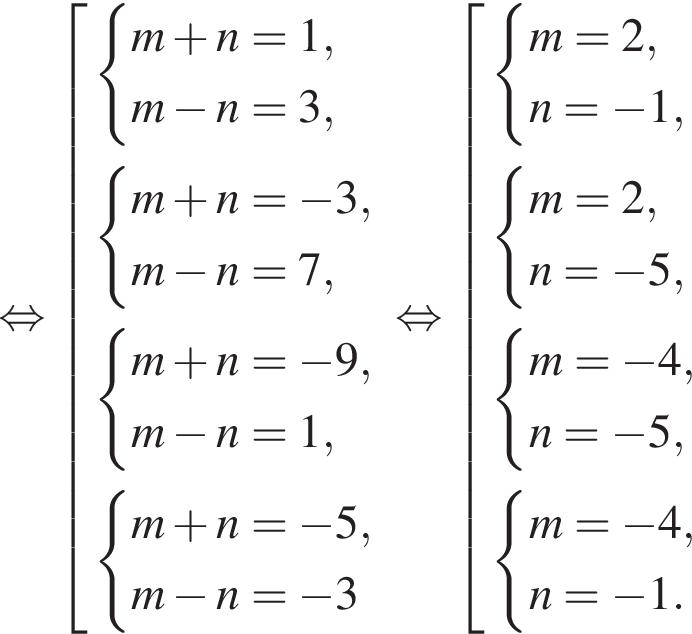
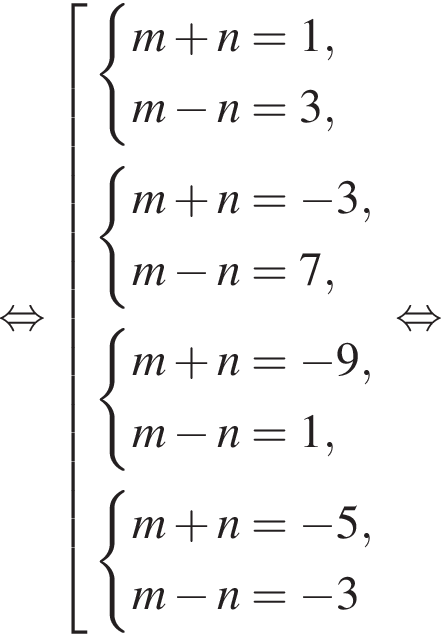
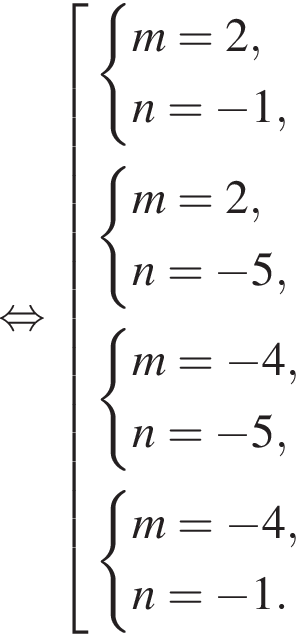
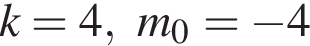 и
и 
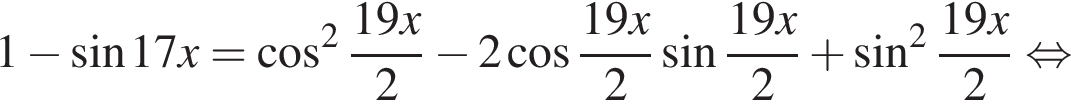
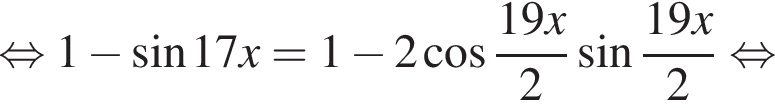
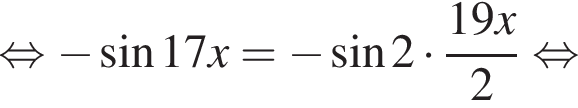
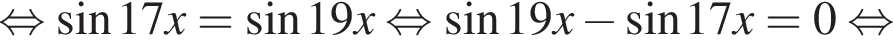
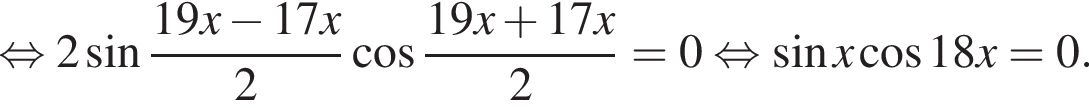
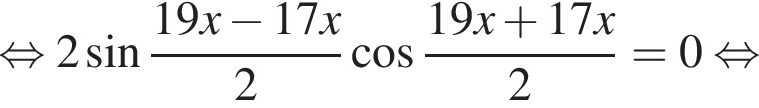



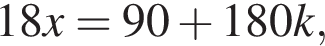 где k целое, то есть при условии
где k целое, то есть при условии 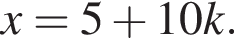 При
При 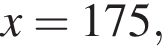 а при
а при 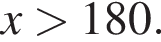
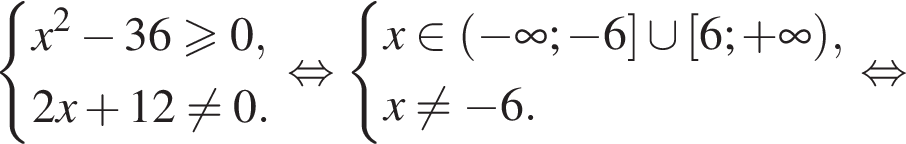

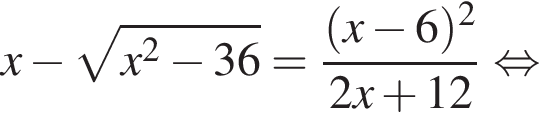
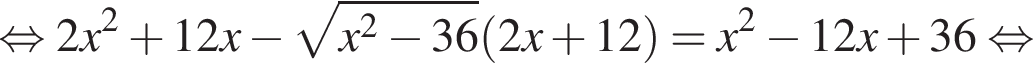
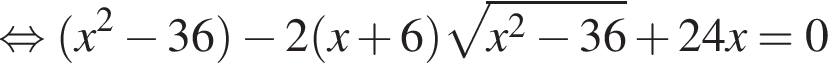
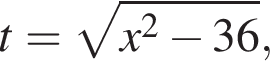 тогда
тогда 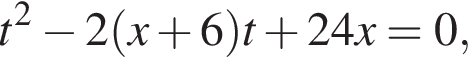 откуда
откуда 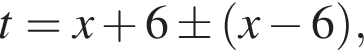 то есть
то есть 
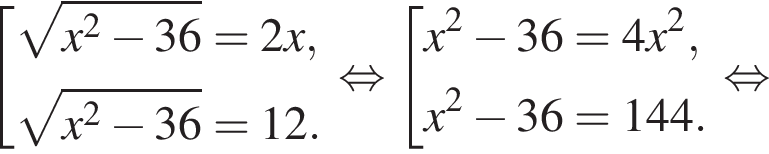
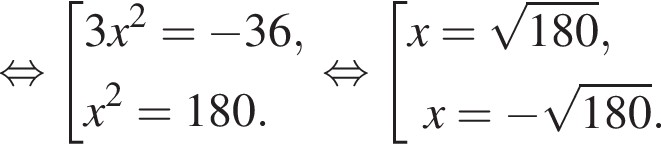
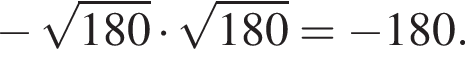
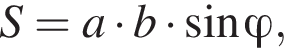 где a и b стороны параллелограмма, а
где a и b стороны параллелограмма, а  а параллелограмм ABCD является прямоугольником. По теореме Пифагора:
а параллелограмм ABCD является прямоугольником. По теореме Пифагора: